If the road is not yet clear to you,
we will show you the way how to get through.

t-test (pairs)

A paired sample t-test is a test for comparing the means of two characteristics.

There are several t-tests. The most common used test is a t-test between the means of two groups, and even of this type there are two subtypes. This is often called a t-test groups. The t-test groups is explained on a separate page of this site.

Another well-known t-test is a test between the means of two characteristics. This is called a t-test pairs. This test is explained on this page of the site.

Finally there is a t-test that tests if a computed mean (or value) differs from a standard. Very often authors refer to this test with one sample t-test. Most often the number 0 is used as the standard. Also this test is explained on a separate page of this site.

t-test pairs

This test is used for research questions like:

- Is the right hand more flexible than the left hand?

- Are the earnings of company higher in December than in June?

- Is the temperature in the living room higher than in the bedroom?

To apply the test you need to have two variables for which it is allowed to compute a mean. A mean can be computed for variables measured at an interval or ratio level. In our first research question these are flexibility in the right hand and flexibility in the left hand. In the second example the two variables are earnings in December and earnings in June. In the third example they are temperature in the living room and temperature in the bedroom. Take care of the criterium that both variables have the same range. If the temperature in the living room is measured in degrees of Fahrenheit and in the bedroom in degrees of Celsius, it makes the variables incomparable.

After detecting the right variables, the difference between the two scores for every element can be computed. This new variable is called Difference, or short: D. You can image that if there is no difference between the scores of both characteristics, the difference score for each element will be zero. This would be a unique because differences almost always will be found. If the scores are not the same, differences will occur. If the mean of all D-scores is 0, then on the average there is no difference between the two characteristics. And finally – and that is what is being tested – if one score is on the average higher than the mean of D will become large. To test if the difference is big enough this formula is used:

One smple t-test formula

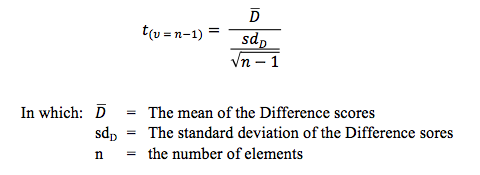
With this formula a t-value is computed. The degrees of freedom for this test are by definition the number of elements minus 1. The computed t-value can be compared with a critical t-value. The critical t-value can be found in a table in any good textbook about statistics (or in Excel). If the computed t-value exceeds the critical t-value, it is said that the test is statistically significant. If this is abracadabra to you, please read our paper about the statistical test procedure where this is explained in detail.

Usually it is okay to apply a t-test pairs if there are 30 elements and if it is allowed to calculate a mean for both variables. If your data do not meet these criteria a Wilcoxon test should be applied.

Use our SPSS tutorials to learn how to run this test in SPSS.

Manuals that help you to significantly improve your research:

Return to the index of this dictionary

Mission

Our goal is to teach you how to conduct good research.

Because:

Good research provides you with better information.
With better information, you can make better decisions.
With better decisions, you can create a healthier, wealthier and freer world,
for people, fauna and flora, for current and future generations.

That is why I think it is important that you know how to do your research well.

If the road is not yet clear to you,we will show you the way how to get through.