Adjusted R-square
Analysing qualitative data.
Analysing quantitative data
ANCOVA (Analyses of covariance)
ANOVA (Analyses of variance)
Applied research
Average
Bias
[...]
Mean
The mean is the sum of all numbers in a list divided by the amount of numbers in that list.
People might quarrel about the best term: is it the mean or is it the average. In my opinion – but maybe I should revise it – is the mean an arithmetic term and average a linguistic term. So, if something has to be computed, the term mean is used and otherwise the term average.
The mean is the average of a serial list of numbers divided by the amount of numbers. For instance, if you have the numbers 4, 5 and 6, then you compute:
(4 + 5 + 6) / 3 = 15 / 3 = 5
That is not difficult, now is it?
This is only a small list of numbers. If you have a long list the principle of how to compute the mean is the same. Instead of explaining this for all lists of numbers, people use a general formula. The complete formula looks like this: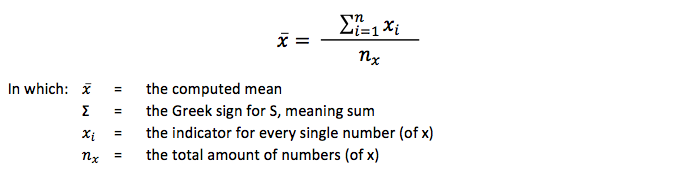
Why is there an x everywhere? Well, a symbol is needed to distinguish this list from other lists. It could be a y to, or a z. But most of all the x is used.
People are lazy – at least I am ... sometimes – and most people use a simplified formula:
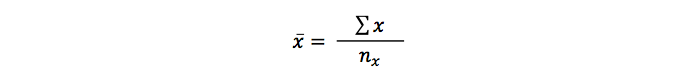
Is this important to know?
Well, it is very basic and you need to know the basics, before we can explain the more difficult things. As you should know, the mean is an indicator of the centrality of a list of numbers. If you have a list of numbers of 104, 105 and 106, the mean of these numbers is 105. Comparing both lists of numbers, you can state that the means are quite different. But that is not always the case. Sometimes the means of two or more list of numbers are almost the same. If they are the same or different should be tested. We will explain that elsewhere, but for now we only explain how a mean is computed.
Another indicator for the centre of a list of numbers is the median. Both indicators might give the same value or a different one. Comparing both values might give a different vision of the centre of the list of numbers.
