If the road is not yet clear to you,
we will show you the way how to get through.

Kurtosis

Kurtosis is an indicator for the flatness of a distribution

A list of numbers can be equally distributed over all possible outcomes or some categories might be more filled than others. In the next three examples this is easily made clear. In the first example there is a distribution that looks similar to the normal distribution. The second one is totally flat and the third one is peaked.

Example 1 of kurtosis

Example 2 of kurtosis

Example 3 of kurtosis

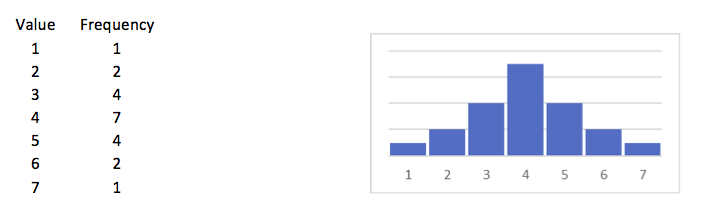
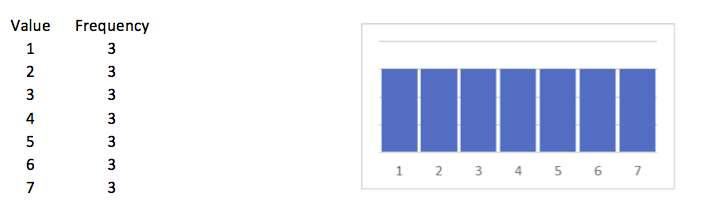
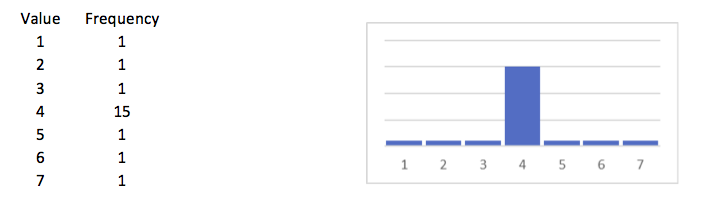
The distributions in these examples have a lot of similarities. They all have 21 objects, the minimum is 1 and the maximum is 7 so the range is 6, and the mean is 4. The remarkable difference is the form of the distribution, and therefore also the standard deviations and the skewness of these distributions differ. These attributes are discussed elsewhere in this dictionary. This page is limited to the kurtosis.

How to compute the Kurtosis

The kurtosis is an indicator for the flatness of a distribution. The question arises: is the distribution flat or does it contain a peak and how does this influence the statistical outcomes. To compute the skewness with this formula:

The formula of Kurtosis

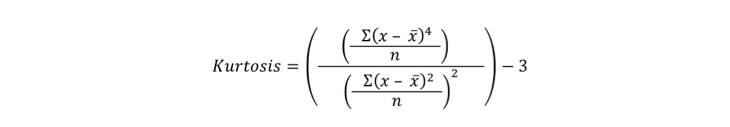
The kurtosis of the distribution in the first example is 0.75, in the second it is -1.257 and in the third it is 3.246.

How to interpret the outcome

In theory, the outcome lies between minus 3 and plus infinite. But that is theory. For the interpretation of the kurtosis, you can use the following as a guide:

Of scores between -0.50 and +0.50 the distribution is said to be about normal
Scores between -1.00 and +1.00 are said to be almost normal
Scores below -1.00 are more flat
Scores over +1.00 are peaked.

What to do when the distribution is too flat or too peaked

To start with the first: a flat distribution is not a problem. A variable needs to differentiate, and if it can make a difference between respondents, subjects or objects. A variable with a flat distribution does what it is designed for: it discriminates.

If the variable is too peaked, it cannot make a difference between the respondents, subjects or objects. Everyone gave the same answer or is belonging to the same group. But when is the kurtosis too high? This also depends on the number of respondents, but in general, variables with a kurtosis over 5.00 are becoming problematic because they cannot make much difference, and variables values with a kurtosis over 10 are useless.

So, I recommend: create variables that discriminate between the objects. The lower the kurtosis the better.

Do you know when to apply which test? Read this manual and you will know it for sure:

How to find the correct statistical test

Return to the index of this dictionary

Mission

My goal is to teach you how to conduct good research.

Because:

Good research provides you with better information.
With better information, you can make better decisions.
With better decisions, you can create a healthier, wealthier and freer world,
for people, fauna and flora, for current and future generations.

That is why I think it is important that you know how to do your research well.

If the road is not yet clear to you,we will show you the way how to get through.