If the road is not yet clear to you,
we will show you the way how to get through.

Normal distribution

The normal distribution is the distribution of a variable in which most scores are in the middle and bell shaped fewer elements are out of the middle.

The best way to explain a normal distribution is by showing it. As you can see in this picture, the top is in the middle and toward both ends the distribution becomes less. In theory the extremes go on into infinity, so the bell shape never ends.

The standard normal distribution

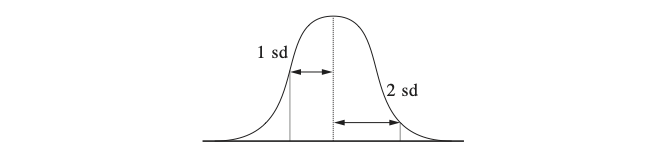
As you might have noticed, there are no numbers at the bottom line. The reason is that there actually are a lot of normal distributions. Every distribution has its own mean and its own standard deviation. Although the shapes of the distributions are equal, the numbers on the bottom line are different for every situation.

The distribution can be used to calculate chances. For example, when filling bottles with milk, an average of one litter of milk enters the bottle. However, the machine cannot always pour exactly 1 litter of milk into the bottle. Sometimes it is a little more, sometimes a little less. What is the probability that 1.08 litters will end up in a bottle?

Another example. Five kilos of potatoes must be put in a bag. Potatoes are not all the same size, so sometimes more comes in the bag. What is the chance that six kilos of potatoes will go into the bag?

To make these calculations, you must use an integral calculus. That is quite difficult. That's why scientists tried to find a formula that could be used as a standard. Many people worked on it, but Gauss and Newton came up with the solution simultaneously but independently. They must have been excellent in mathematics, because the formula of this distribution is this:

Norman distribution - formula

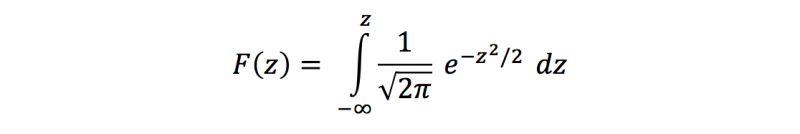
Please don’t be afraid of this formula. It is not necessary to know any formula to become a good statistician. It is not even necessary to be able to make calculations yourself, though it is a pre if you understand the arithmetic of statistics. This formula is only shown here to make clear that an z is calculated.

The distribution of Gauss and Newton is called the standard normal distribution and has a mean of 0 and a standard deviation of 1.

Every normal distribution can be converted to the standard normal distribution by subtracting the mean of each score and divide this by the standard deviation. In a formula it looks like this:

How to standardise the scores to a standard normal distribution

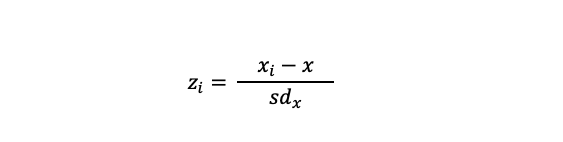
Again, you do not have to do the calculations yourself. Computer programs can do this for you.

How is the normal distribution used in statistics?

In statistics the standard normal distribution is used for calculating chances. To see how it works, you need to understand one thing very clearly: the total surface under the curve is 100%. That is not too difficult to understand. The second thing that is important to know is that the surface on the left to 0 is 50% and the surface on the right to 0 is also 50%. That should not be too difficult to understand as well. And finally, the surface between two z-scores can be calculated as a percentage. Even this isn’t difficult to understand. The calculations however are very heavy. This is done with integral calculus (fortunately we have computers nowadays).

To give some examples, the percentage surface between the z-sore -1 and +1 is 68,26%. The percentage surface left to the z-score +2 is 97,72%. For every z-score the percentage can be calculated. They can also be found in any good textbook about statistics or in Excel. We already made these tables. You can download our Excel-file withe the critical values from the right side of this page.

You only need to remember some values of the normal distribution

Though there are a lot of z-scores for which the surface under the curve can be computed, there are only a few that are really important. This has to do with the fundamentals of statistics. Mr R.A. Fisher, one of the founders of modern statistics, argued that only chances of 5%, 1% and 0.1% are important. (Learn more about the statistical test procedure in our paper.) The z-scores of these percentages are called the critical values. You can read these values in the table below.

Relevant z-scores of the normal distribution

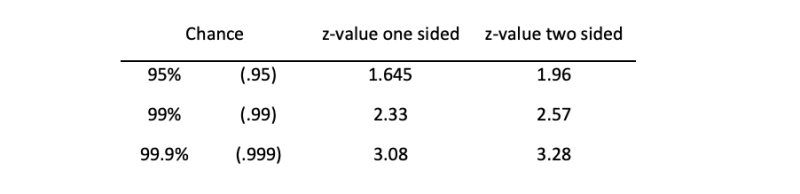
How to use this table

A lot of research questions have a form like A is larger than B. Now you can compute A and B. If A is bigger than B, you might conclude it is a good statement. However, there is always a chance you are wrong, and small differences are not of importance. When is a difference large enough?

Now if you compute the z-score with a formula (and there are quite a number of statistical tests that compute a z-score), you can compare this computed z-score with the critical z-value in the table. If the computed z-score exceeds the critical z-score it is said that the difference is statistically significant.

Final comments

Though the standard normal distribution is basic, it is not the most common distribution in statistics. It seems to me that the t-distribution, the chi square distribution and the F-distribution are used more often. All these distributions are derived from or have relations with the standard normal distribution. We will discuss these distributions elsewhere in this dictionary.

Use our SPSS-tutorials to analyse your data. It will go much faster.

Read these manuals to undertand the basics of statistics:

Return to the index of this dictionary

Mission

My goal is to teach you how to conduct good research.

Because:

Good research provides you with better information.
With better information, you can make better decisions.
With better decisions, you can create a healthier, wealthier and freer world,
for people, fauna and flora, for current and future generations.

That is why I think it is important that you know how to do your research well.

If the road is not yet clear to you,we will show you the way how to get through.