If the road is not yet clear to you,

we will show you the way how to get through.

The standard deviation is an indicator for the dispersion in a list of the numbers. The value 0 means that there is no dispersion at all.

If you have a list of numbers most probably not all numbers are the same. One way to describe this list of numbers is to calculate the mean. The mean is a good indicator for the centre of this list of numbers. But a list with the numbers 8, 9, 10, 11 and 12 is different than a list of numbers 4, 7, 10, 13 and 16. The mean of both series is 10. But it is not hard to notice that the numbers in the first list are closer to each other than in the second list. Is there an indicator for this dispersion?

But of course there is. You can calculate the difference for each number with the mean. For the first list this is: -2, -1, 0, 1 and 2. If you sum these numbers the total is … 0! Yes indeed, it is exactly zero. And this will always be the case. You might try it for the second list.

A better indicator is to square the differences. Than you get (8 – 10)2, (9 – 10)2, (10 – 10)2, (11 – 10)2, and (12 – 10)2. If you sum these values you calculate (4 + 1 + 0 + 1 + 4 =) 10. The problem is, if you have more numbers in a list, the indicator for the dispersion will continue growing while you can see that the dispersion is not changing at all. For instance, in the list of 8, 8, 9, 9, 10, 10, 11, 11, 12, and 12 the dispersion is the same, but if you calculate with the given formula the total dispersion will be (4 + 4 + 1 + 1 + 0 + 0 + 1 + 1 + 4 + 4 = 20). The solution for this problem is simple: divide the outcome by the total amount of numbers in the list. The dispersion in the first list is then: (10 / 5 =) 2 and in the list with the double amount of same numbers it is (20 / 10 =) 2. This is a good indicator.

This can be put is a general formula. It looks similar to the formula of the mean:

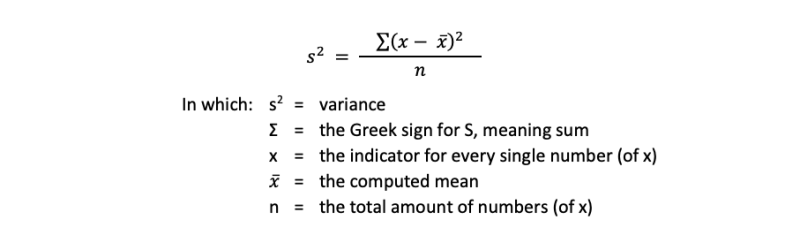
Oops, there is still something wrong. Did you notice we wrote an s2? What has been calculated here is not the standard deviation but the variance. The variance is an indicator for the dispersion too. As a matter of fact, the standard deviation and the variance are directly related to each other. The standard deviation is the square root of the variance. So the correct formula for the standard deviation is:

Why is there an indicator for dispersion named variance and standard deviation?

Good question. In statistical analysis the variance is usually used and the calculations are just one step less than with the standard deviation: you don’t have to calculate the square root. However, the standard deviation is easier to interpret.

As a rule of thumb you can calculate a minimum and a maximum of the range of the list of numbers as 2 or 3 times the standard deviation. For our first list – 8, 9, 10, 11 and 12 – the calculated minimum is (10 - 2 * √2 =) 7.2 and the calculated maximum is (10 + 2 * √2.4 =) 12.8 For the second list – 4, 7, 10, 13 and 17 – the calculated minimum is 0.9 and the calculated maximum is 19.1. As you can see this is an overestimation. Normally the calculated minimum and maximum are closer to the real minimum and maximum values. However, if you calculate this with the variance, you will get values that are not easy to interpret.

How to interpret the standard deviation

The outcome of the formula is minimal zero (0), but there is no maximum. If the outcome is zero, it means that there is no dispersion. In other words: all numbers have the same value. A variable with no dispersion has no variation. It is a constant.

If the outcome is low it means that a lot of numbers are close to the mean. It is impossible to make a statement which values are low. It depends on the range of the numbers. If the range is 4 (for instance with a five point Likert scale) a standard deviation about 0.8 is a rather normal outcome. If the range is 60 (for instance age) a standard deviation of 15 is then rather normal.

Again you can use the rule of thumb: four to six times the standard deviation should be almost equal to the range. It has to be stressed that this rule of thumb is indicative. A lot more can be of relevance. For instance if there are a lot of numbers close to the mean and only a few numbers far away from the mean, then this rule of thumb doesn’t give a very clear insight of the dispersion. On the other hand, this rule can be used to identify outliers. Outliers are numbers that are far from the mean and can be of big influence on the outcome of a statistical analysis.

And one more thing …

There is one more thing that is very important to notice here. The calculation above is correct when it is applied to the total population. Huh? What do you mean?

If you have a list of numbers that is exactly the total amount of numbers you can find in the population (there are no more and no less), than the formulas are applicable. However, not an s should be used but a σ (sigma), the Greek symbol for the letter s. However if the list of numbers is a sample of the total amount of possible numbers, than statisticians divide by n – 1 instead of only an n. This is due to sampling error and has to do with the degrees of freedom. Look for more information about this issue on these pages.

Related topics to Standard Deviation:

• Mean (or average)
• Median
• Mode
• Skewness
• Kurtosis
• Outliers
• Sampling
• Degrees of freedom

Analyze your data quick and easy with our SPSS tutorials.

Recommended paper to conduct excellent research:

• How to choose the correct statistical test
• The statistical test procedure
• Presenting statistical results

Return to the index of this dictionary