If the road is not yet clear to you,

we will show you the way how to get through.

Four distributions are very commonly used in statistics: the standard normal distribution, the t distribution, the chi-squared distribution and the F distribution. The z-value is calculated for the standard normal distribution.

A lot of aspects in real live show a normal distribution. An examples is filling bottles with one liter juice. Though the machine might seem to work perfect, some bottles are filled with a little bit more liquid and others with a litle bit less. All in all and on the average there will be one liter of liquid in every bottle.

Meuasuring a 1000 bottles, the volume of the bottles are normally distributed. However, normal distributions aren't very easy to use in statistics. Therefore they are transformed into the standard normal distribution. This formula is used for it:

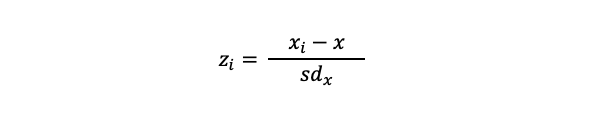
As you can see a z is calculated. This is the z-value of the standard normal distribution. This z-value is used for statistical tests.

A lot can be told here about statistical tests.If you are unfamiliar with statistical testing I suggest te read my paper about the statistical test procedure. In short, the calculated z-value is compared with the critical z-value of the normal distribution. If the calculated value exceeds the critical value, the result is called statistically significant.

The critical z values can be found in a table. Such a table can be found in any good statistical textbook or can be downloaded from this site.

Suggestions for further reading:

• normal distribution 
• t-distribution 
• chi square distribution 
• F-distribution

Manuals that help you to significantly improve your research:

• How to find the correct statistical test 
• The statistical test procedure 
• How to present statistical results

Return to the index of this dictionary