If the road is not yet clear to you,

we will show you the way how to get through.

Kendall’s tau is the unity for the strength of cohesion between two ordinal variables.

It is very important to find out whether a relationship exists between variables. If the value in variable A increases and so does the value in variable B, there is a relationship. The strength of this relationship is determined by calculating a measure of correlation or association. For continuous data, this is Pearson's product moment correlation. For ordinal data, usully the Spearman rank correlation is usually calculated. For nominal data, Cramérs V is usually calculated.

An alternative for the Spearman rank correlation is Kendall’s tau.

The formula of Kendall's tau

Kendall’s tau is computed with this formula:

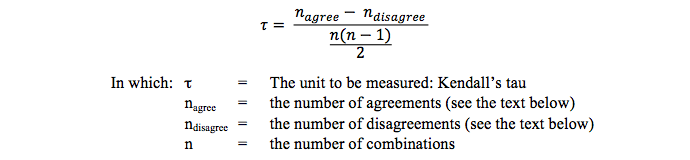
The outcome of this formula has a minimum of -1 and a maximum of +1 and can be interpreted in exactly the same way as for the product moment correlation of Pearson or the rank-correlation of Spearman. -1 indicates there is a perfect negative relationship: if the value of variable A increases, the value of variable B decreases. +1 indicates there is a perfect positive relationship: if the value of variable A increases, the value of variable B increases too.

An example of the computations

Suppose two teachers judge ten books that could be used for their lessons. They order the preference for each book from best to worst. If both teachers judge the books equally no differences would be seen and tau would be 1. This may hardly ever be the case. If there is a lot of agreement this can be scored by calculating Kendall’s tau. This is how it is done.

The preference list of one teacher is used as a reference and ordered from best to worst. The preference list of the second teacher is written next to it. Suppose the ranking looks like the one in the table below.

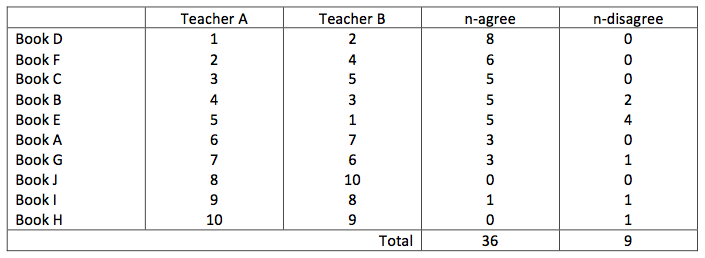
Now two extra columns are produced.

In the first column the number of agreements is written. This is the number of books with a higher rank order in the list below of the second teacher. (I always had problems with understanding this correctly. An example might help. Book D was ranked by teacher B as second best. The numbers below with a higher ranking score are: 4, 5, 3, 7, 6, 10, 8 and 9. In total 8 books. So we write 8 in the list of n-agree.)

In the second column the number of disagreements is written. This is the number of books with a higher ranking in the list above of the second teacher. Again it has to do with a higher score. This starts with book B: only the numbers 4 and 5 are higher than the score 3 in the list of teacher B.

This was the most difficult part. Mistakes are easily made. To check the outcome of the number of agreements and disagreements, one can add these two numbers. The outcome should be equal to n * (n - 1) / 2. In this example it is (10 * (10 - 1) / 2 = 45.

The numbers in the columns of agree and disagree have to be added and putting these numbers in the formula, Kendall’s tau can be calculated. In this example it is:

tau = (36 - 9) / ((10 * (10 - 1) / 2) = .60.

Alternative formula’s for Kendall’s tau

Because adding up n-agree and n-disagree is always equal to n * (n - 1) / 2, two alternative formula’s can be given for calculating Kendall’s tau:

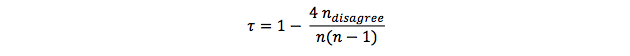
                        or:

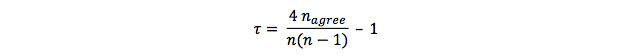
Testing the strength of Kendall's tau with statistics

To test the strength of the relationship between te two variables, this test is used:

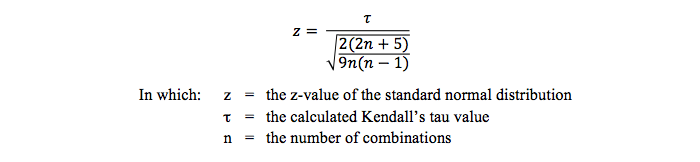
Related topics to Kendall's tau

• Pearson product moment correlation
• Spearman rank correlation
• Cramérs V
• Variable

All these tests are clearly explained in in our SPSS-tutorials.

These manuals make it easy to work with statistics:

• How to find the correct statistical test
• The statistical test procedure
• How to present statistical results

Return to the index of this dictionary