If the road is not yet clear to you,

we will show you the way how to get through.

Cramers V is the unit for the strength of cohesion between two variables measured at a nominal level. The contingency table is not necessarily square. It is possible to calculate Cramers V for rectangular tables too.

Is it Cramers V or Cramérs V?

First I want to comment on the name. In English all reading signs on the letters are deleted. As far as I know, the correct name is with a strike above the e. However, in this dictionary we don't makes use of strikes too. Therefore the name is written without a strike in this dictionary.

How to compute Cramers V

The value of Cramers V is calculated with this formula:

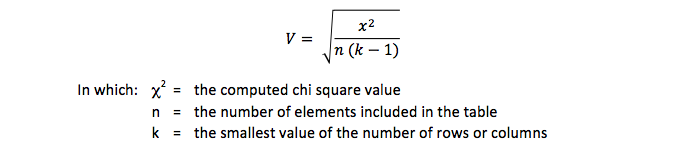
The outcome of this formula is always between 0 and 1.

How to interpret Cramers V

The beauty of Cramers V is the comparability of interpreting the outcome with the correlation coefficient of both Pearson and Spearman.

The value 0 means there is no cohesion between the two variables. The numbers are proportionally equally divided over the cells. The term proportional is important, because the numbers in the cells should be proportionally in accordance with the row or column totals (see the examples below).

A Cramers V value of 1 means a perfect correspondence. All values in a row are also in one cell of a column.

Because we are dealing with variables measured at a nominal level, the rows or columns can be reversed without any problem. Now it is easy to show that with a perfect relationship only the cells in the diagonal are filled. Due to this reversibility it is not important if the cells in the diagonal are filled from left above to right down or from left down to right above. The sign (that is minus (-) or plus (+)) is not important.

Examples of Cramers V

The examples below show an increasing value for Cramers V. The first example shows a value of 0 and the final one a value of 1. The one in the middle shows a value somewhere in between. Please pay attention to the change in the number of elements in each cell. (By the way, these tables are made with fictional numbers.)

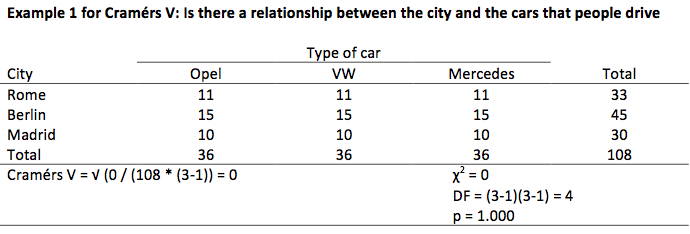
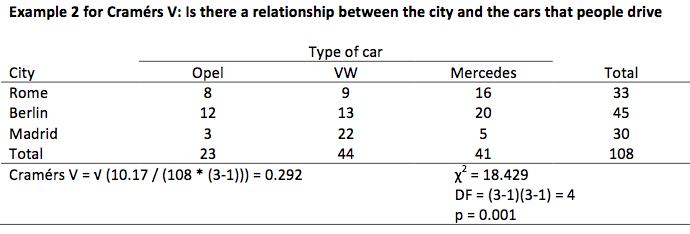
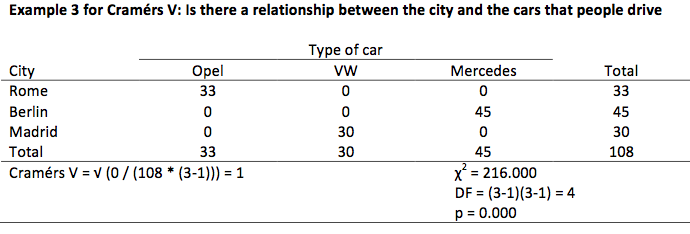
Testing Cramers V

Cramers V is tested with the chi square test. This is a little bit odd, because the chi square value is also part of the formula for computing Cramers V.

How to compute Cramers V in SPSS can be found in our SPSS-tutorials.

Related topics to Cramers V:

• Pearson product moment correlation
• Spearman rank correlation
• Kendall’s tau
• Phi coefficient
• Variable 
• Nominal level

Manuals that help you to significantly improve your research:

• How to find the correct statistical test
• The statistical test procedure
• How to present statistical results

Return to the index of this dictionary