If the road is not yet clear to you,

we will show you the way how to get through.

The Spearman rank correlation is the measurement unit for the strength of cohesion between two variables measured at an ordinal scale.

It is very important to find out the relationship between variables. If the value in variable A increases and the value in variable B too, there is a relationship. The strength of this relationship is determined by computing a correlation coefficient. For continuous data the product moment correlation of Pearson is used. For ordinal data the Spearman rank correlation is calculated with this formula:

It may look odd, but the outcome of this formula has a minimum of -1 and a maximum of +1.

The outcome can be interpreted exactly in the same way as for the product moment correlation of Pearson. -1 indicates there is a perfect negative relationship: if the value of variable A increases, the value of variable B decreases. +1 indicates there is a perfect positive relationship: if the value of variable A increases, the value of variable B increases too. If you make a plot of this relationship all dots are in a straight line. The outcome 0 means there is no relationship at all between these two variables. Scores between 0 and +1 and between 0 and -1 are indicative for the strength of the relationship.

Like in the product moment correlation of Pearson the strength of the relationship can be tested with (almost) the same formula:

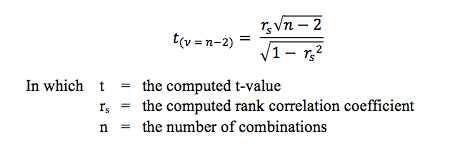
This formula is testing if Spearman rank correlation is unequal to 0. Testing can be done two-sided or one sided. Read more about statistical testing in our paper/manual about The statistical test procedure.

Some statisticians complain that the Spearman rank correlation is basically a unit of measurement for data measured at interval level because the difference (the d in the first formula) between two scores is computed. This makes the Spearman rank correlation pretty well comparable with the product moment correlation of Pearson. According to these statisticians Kendall’s tau should be computed for ordinal data. Basically they might be right, but daily practice shows that almost always the Spearman rank correlation is used.

Learn how to analyze your data quick and easy with our SPSS tutorials.

Related topics to Spearman Rank Correlation.

• Pearson Product Moment Correlation 
• Kendall’s tau 
• Cramer’s V 
• Variable 
  • Nominal level 
  • Ordinal level
  • Interval level 
  • Ratio level

Manuals that help you to significantly improve your research:

• How to find the correct statistical test 
• The statistical test procedure 
• How to present statistical results

Return to the index of this dictionary