Hierarchical regression

Hierarchical regression analysis is a technique that compares two regression lines to find out which one explains a phenomenon the best.

In multiple regression a list of predictive variables is used to predict an outcome. Factors like motivation, time spent on learning, intelligence, familiarity with the subject and so on, are all very likely to predict a score on a test. The equation for the multiple regression line is this one:

hierarchical regression - 1

The formula can be made as long as you wish by adding more predictors in the equation. Depending on your time, money and the motivation of people to participate in your research, tens or even hundreds aspects can be measured. Most likely all these aspects do not contribute all to predicting an outcome. Which aspects do have an impact and how do you conclude if a variable should be included or excluded.

To explain the comparison in a less abstract way an example is used with three aspects. The first aspect is motivation(x1), the second one is time spent on studying (x2) and the third one is intelligence (x3). You might wonder if adding the variable intelligence would improve the equation and make better predictions. Measuring intelligence is not easy, and if it does not contribute to explaining the predicted score, a lot of money can be saved. In short, two regression lines have to be compared:

hierarchical regression - 2

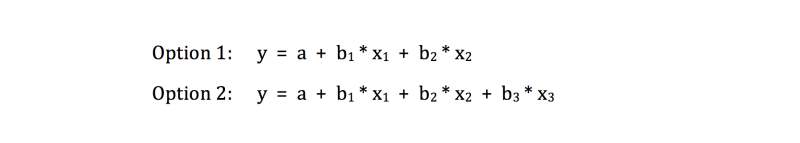
To compare both options, look at the change in the multiple correlation coefficient (R2) and the change in the regression coefficients.

The change in R²

Adding predicting aspects always leads to a higher R². The question is, is the change in R2 of option 1 and option 2 statistically significant. More concretely, does intelligence improve the equation and does it lead to a better predicted score in the test.

To test this, the difference between R² in option 1 and 2 is computed (notated as ΔR2), and tested with an F-test. If the outcome is statistically significant, you have a good argument to include intelligence as an explaining aspect. If it is not statistically significant, it can be omitted.

Working this way, the effect of adding every single aspect (or a list of aspects) can be tested. A very common list of variables to be put in the equation, are the variables to be controlled for. In our example this might be gender, age and education level. Put them in first and then the predictive variables. Now the change in R² indicates if the predictive variables contribute to explaining the result.

The change in the regression coefficients

Adding or omitting a variable has an effect on all regression coefficients. An aspect that was statistical significant in one list of variables, may lose its statistical support in another list. Even the opposite might happen: adding a new aspect may change a variable from not-statistically significant into statistically significant. Therefore, always study the outcome carefully.

Theoretical and practical relevance

Hierarchical regression analysis is a good technique to test theories. Adding or omitting aspects might support one theory and disapprove another. It can lead to a nice theoretical framework in explaining what is happening.

Daily life might give a different view. The theoretical framework may not correspond with real life. Several reasons can be mentioned. It takes time to build a theoretical framework, and at the time the framework should be used for making decisions, real life has changed. For instance, if a theory about shopping behaviour has been worked out for a shop in the centre of a town, the behaviour of consumers may have changed to online shopping. Or, the sail of cars may change due to a change in economic welfare and ecological attitude. Another list of reasons can be found in external validity. The regression model may be applicable to the European situation, but not to the American or Asian situation. And finally a change in numbers of participants or the way in which way the variables are being operationalized, might lead to another regression model. Only when the model shows the same outcome in several researches, it is a good model to predict an outcome in daily life. But beware, sometimes it is not. There will be always aspects that detract from the prediction.

If the road is not yet clear to you,
we will show you the way how to get through.