If the road is not yet clear to you,

we will show you the way how to get through.

The chi-square test for contingency tables is used to find out whether the observed numbers are equally distributed over the cells.

An example of a chi-square test for contigency tables

Suppose you want to find out if boys and girls are equally able to swim. So you ask them two questions Are you a boy or a girl? and Can you swim? The answers can be split out in a table:

It looks like more girls can swim but somehow more girls have been questioned. Therefore the absolute numbers might give a wrong impression. We will take a closer look at that later on, for now we are only interested in the statistics. The question to be answered is: do boys and girls differ in the ability to swim?

How to test this contingency table

To test this question a statistical analysis is performed, in this case a chi-square test for contingency tables. The formula to be used is this one:

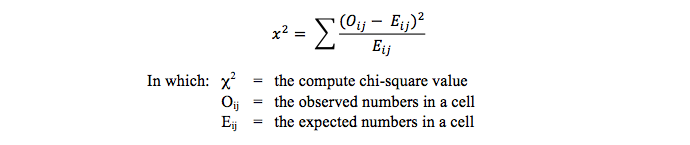
The observed numbers (Oij) can be read from the table, but where can the expected numbers (Eij)? Well, the expected numbers for each cell have to be calculated. This calculation is rather easy. This is the product of the row and column totals divided by the grand total. For the cell Boy-Yes this is (112 * 157 / 400 =) 43.96. A new table can be produced with these numbers.

Just notice the row and column totals are still the same as before.

Now the formula can be filled in and we get:

The outcome of the computed value can never be negative (a squared value is always positive). Now the test procedure can be finished. The computed value (5.16) is compared with the critical value of the chi-square distribution. To find this value we need to know the degrees of freedom. For contingency tables the degrees of freedom are computed as (the number of rows minus 1) times (number of columns minus 1). That is (2 – 1) * (2 – 1) = 1. The critical chi-square value is 3,84 (for alpha is 0.05) 6.63 (for alpha is 0.01) and 10.82 (for alpha = 0.001).

OK, boys and girls differ in swimming ability. But can more boys swim than girls? For this a new table is produced with percentages.

Now it is more obvious: more girls can swim than boys.

Final remarks about this chi-square test

The text above is based on a simple example and I hope this has explained a lot. The procedure can be done for any kind of contingency table. The example used was a 2 x 2 table, but any table will do.

Real statisticians – I mean the diehard statisticians – demand that the minimal expected value should be 5. I like to stress it is the expected value, not the observed value. They use the argument that computing the outcome will be unstable when there are too few numbers. This may be true, but not enough cases is not the only problem for the chi-square test. It is a problem for all sorts of statistical analysis. Besides that, it is difficult to find an alternative analysis. So – in my opinion – don’t take that too much in account.

The above procedure is in accordance with the statistical test procedure as used worldwide. Statistical software however does not often present the critical values. They show the exact p-value. For our example the exact p-value is 0.023. The conclusion to be drawn is still the same: more girls than boys can swim.

In in our SPSS-tutorials we clearly explain how to analyse a contingency table.

Related topics to chi-square test for contingency tables

• Normal-distribution
• t-distribution 
• Chi-square distribution 
• F-distribution 
• Chi-square test 
• Chi-square test for frequencies 
• Phi-coefficient 
• Cramer’s V 
• Degrees of freedom 
• p-value

Deepen your knowledge and read our manual about ...

• The statistical test procedure 
• How to choose the correct statistical test

Return to the index of this dictionary