Adjusted R-square
Analysing qualitative data.
Analysing quantitative data
ANCOVA (Analyses of covariance)
ANOVA (Analyses of variance)
Applied research
Average
Bias
[...]
Phi-coefficient
The phi-coefficient is a value that indicates the strength of cohesion between two dichotomy variables, so only for a 2x2-table.
The formula of the phi-coefficient
There are two formulas for the phi-coefficient:
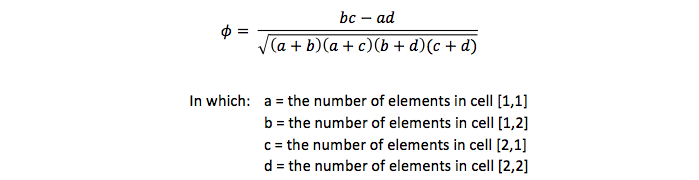
and
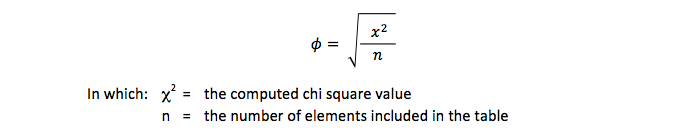
Although both formulas look very differently computations with the same data give the same outcome.
The second formula is similar to the formula of Cramérs V. Therefore the phi-coefficient can be seen as a special case of Cramérs V.
How to interpret the phi-coefficient?
The outcome of this formula is always between 0 and 1. The value 0 means there is no cohesion between the two variables. The value 1 means a perfect correspondence: only the cells on the diagonal are filled.
Because we are dealing with variables measured at a nominal level, the rows or columns can be reversed without any problem. Due to this reversibility it is not important if the cells in the diagonal are filled from left above to right down or from left down to right above. The sign (that is minus (-) or plus (+)) is not important.
Testing the strenght of the phi-coefficient
The phi-coefficient is tested with the chi square test. This is a little bit odd, because the chi square value is also part of the formula for computing the phi-coefficient too.
An example of computing the phi-coefficient
One might wonder if women more often take a course on self-defence than man. Now two variables are needed: gender (woman = 1, man = 2) and did take the course (no = 0, yes = 1). For 98 youngsters between 15 and 30, these numbers were found:
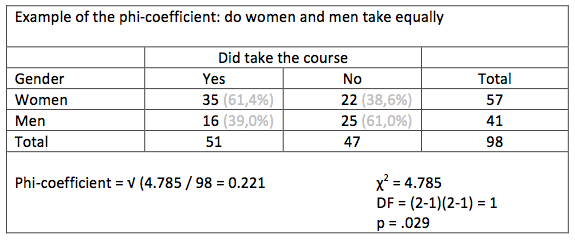
Without the percentages the differences are not easily seen. It really helps to interpret the result.
Use our SPSS tutorials to learn how to run this test in SPSS.
