If the road is not yet clear to you,
we will show you the way how to get through.

Chi square test for frequency distributions

The chi-square test for frequency distributions is used to test wether an observed frequency distribution equals an expected frequency distribution.

An example of a test about frequency distribution

Suppose 100 student can choose one from the four tutorials about statistics. It there is no preference the expected values would be equally divided, that is every tutorial is attended by 25 students. When the tutorials started, you might count the students in every tutorial. Not surprisingly, the students aren’t equally divided over the tutorials. We are not interested in the reasons why (a better teacher, more friends, better classroom, better schedule?), but just want to know if the observed numbers really differ from the expected equal distribution.

To picture the situation more clearly a table is produced:

Frequencie for chi-square distribution

Small differences can always occur, and if that is small, it would be close to zero. But in this situation, tutorial C looks popular and attracts more students. The difference is not close to zero, but much more. Is this statistically significant?

The calculations to test the difference in a frequency distribution

When you calculate the difference the value is ( -7 + -2 + 15 + -6 = ) 0. This will always be the case in comparing lists of observed and expected numbers. To avoid the summation of the differences will be zero the values are squared. This however leads to large numbers. Therefore the squared differences are divided by the expected numbers and these values are summed. The table below shows the calculations being made: Frequencie for chi-square distribution

If you want to know if the value 12.56 is far more than 0 it has to be compared with other values. For this, the chi-square distribution is used. Why? Just because no negative outcomes can occur, so the normal distribution and the t-distribution cannot be used. The chi-square distribution fits perfectly. The calculated outcome can never be less than zero and the maximum can be very large. Try this yourself by imagining some scores and computing the outcomes.

The computed value can be compared with a critical value in the chi-square distribution. This value can be found in the table of critical values of the chi-square distribution, but which line in the table is the right one? You have to know the degrees of freedom to. In our example the degrees of freedom are (4 tutorials minus 1 is) 3. There the values are found for alfa is 0.05, 0.01 and 0.001 and are respectively 7.81, 11.34 and 16.27. Now the conclusions can be drawn that the value 12.56 exceeds the value of 11.34 so it is statistically significant on alfa is 0.01. The conclusion to be drawn is that tutorial C attracts more students. We still don’t know the reason why, so it is not allowed to conclude that tutorial C has a better teacher, is chosen because friends go there too, is in a better classroom or fits better in the agenda of the students.

The above procedure is in accordance with the statistical test procedure as used worldwide. Statistical software however often does not present the critical values. They show the exact p-value. The conclusion to be drawn is still the same: the difference in numbers of students over the four courses isn’t equally divided.

The general procedure

Above is based on an example and I hope this has explained a lot. For avoiding difficult computations simple numbers have been used. The expected numbers don’t have to be distributed equally over the cells, any other distribution might be stated. So instead of 25 – 25 - 25 – 25 also 20 – 20 – 40 – 20 might be stated. In this situation, I don’t think a statistically significant result will be found. If you like, try to do the computations yourself.

The general formula for computing the chi-square is this one:

Chi-square distribution formula

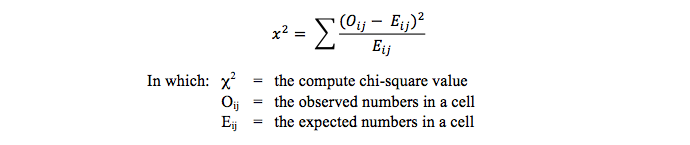
This procedure can be used in which an observed distribution has to be compared with an expected distribution. This should be done, for example, by comparing the numbers in the response with the numbers in the population to see if the response is representative. Very often this test is being omitted for unknown reasons, which causes conclusions to be drawn in a rather hazardous way.

In our SPSS-tutorials we clearly explain how to analyse frequency distributions.

Manuals that help you to significantly improve your research:

Return to the index of this dictionary

Mission

My goal is to teach you how to conduct good research.

Because:

Good research provides you with better information.
With better information, you can make better decisions.
With better decisions, you can create a healthier, wealthier and freer world,
for people, fauna and flora, for current and future generations.

That is why I think it is important that you know how to do your research well.

If the road is not yet clear to you,we will show you the way how to get through.