If the road is not yet clear to you,
we will show you the way how to get through.

Mann-Whitney test

The Mann-Whitney test is used for comparing the scores of two groups on one variable measeured on an ordinal scale.

A variable measured at ordinal, interval or ratio level can be ranked from high to low. The best gets number 1 and the second best gets number 2 and so on. These ranking scores can be divided into two groups. Now the question rises whether one group has a higher mean than the other group. To test this statistically a Mann-Whitney test is applied.

Examples of research questions for the Mann-Whitney test

This test is used for research questions like

Do boys run faster than girls?
Do people in the Netherlands judge the weather better than in Finland?
Do households with children use more electricity than households without children?

To test these questions two variables are needed.

The first one is the grouping variable with only two values (a dichotomy). In the first research question this is gender (boys and girls). In the second research question this is country (The Netherlands and Finland). In the third research question this is type of household (with or without children). This grouping variable is always measured at a nominal level with two values - this is the independent variable. If there are three or more values the Kruskal-Wallis test should be applied.

The dependent variable is a variable measured at ordinal, interval or ratio level. Variables measured at the interval or ratio variables can always be converted into ordinal variables. Therefore the Mann-Whitney test can also be applied to these kinds of data. In the first research question this can be operationalized as the time in seconds to run 100 meters. Afterwards this is transformed into fastest, second, third and so on. For the second research question the answers were collected on a five point rating scale, with 1 = very bad to 5 very good (a Likert scale). This is already a variable measured at ordinal level and it does not have to be transformed. The amount of used electricity is the dependent variable in the third research question. This has to be converted into a variable on ordinal level too.

The calculations of the Mann-Whitney test

After ranking the scores they are split up in the groups. Next these ranking scores are added for each group. If the sums of added scores are equal, there is no difference between both groups. (This is only true if the sizes of both groups are equal.) To test if the summed scores differ a U-value (that is why this test is often denoted as a Mann-Whitney U-test) is calculated with this formula:

How to calculate the Mann-Whitney U

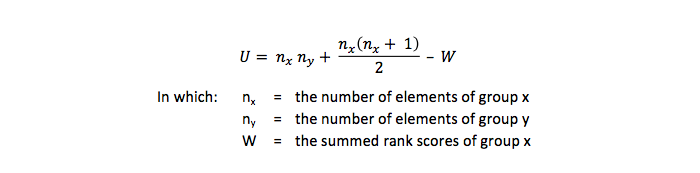
This U-value is tested with this formula:

Testing the Mann-Whitney U

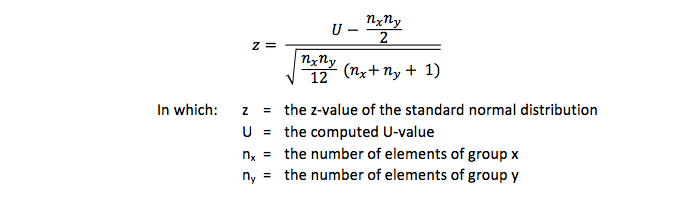
However if ties exist (a tie is an equal rank score) this formula should be used:

Testing the Mann-Whitney U with ties

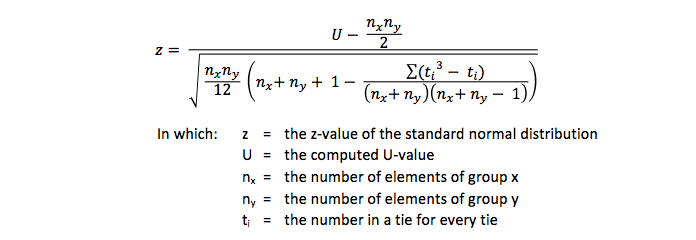
Statisticians recommend to have at least 20 respondents / subject / objects in each group and both groups should be fairly equal in size. With larger group sizes - say above 30 each - a t-test (groups) is recommended.

It is unclear what to do if the group sizes differ considerably. A crosstab can be created and applying a chi square test might give more insight - especially on a five point Likert scale - and maybe it is even better to conduct a t-test with unequal variances.

Use our SPSS tutorials to learn how to run this test in SPSS.

Read these must-have manuals to improve your research:

Return to the index of this dictionary

Mission

My goal is to teach you how to conduct good research.

Because:

Good research provides you with better information.
With better information, you can make better decisions.
With better decisions, you can create a healthier, wealthier and freer world,
for people, fauna and flora, for current and future generations.

That is why I think it is important that you know how to do your research well.

If the road is not yet clear to you,we will show you the way how to get through.