If the road is not yet clear to you,

we will show you the way how to get through.

Cohen's Kappa is a coefficient of agreement between two raters or - more general - between two variables. The maximum score is 1 meaning that a total agreement is reached. There is no minimum.

Suppose two specialists in behaviour have to classify busy children into the categories PPDNOS, ADHD, None or Both. Each child in the entity gets scores from both specialists. Between these two specialist a cross table can be made, something like this:

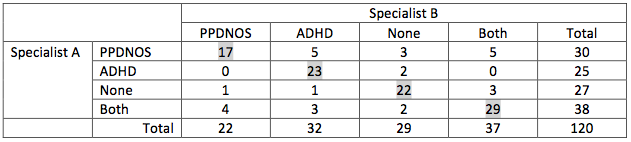
It is obvious that there is some agreement, but it is not a total agreement. The phi-coefficient does not fit because it is not a 2 x 2 table. Cramer’s V might fit, but we are interested in the agreement and not in the amount outside the diagonal. And Kendall’s tau is a coefficient of agreement too, but is applicable to ordinal data. These data aren’t ordinal. We are looking for a coefficient that is only concerned about the diagonal. The coefficient who is applicable is Cohens Kappa.

The computation of Cohens Kappa is not too difficult. It takes three steps.

Step 1: Compute the percentage of agreement, that is the numbers on the diagonal divided by the total. In this case it is ( (17 + 23 + 22 + 29) / 120 =) 75.8%.

Step 2: Create an expectation table in percentages for the cells on the diagonal. The expected percentage is the row-total times the column-total divided by the grand total. For PPDNOS this is 30 * 22 / 120 = 5.5.

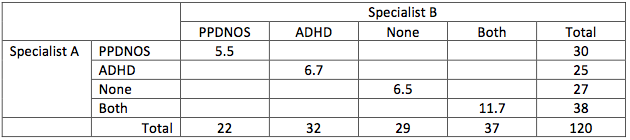
The percent of agreement in this table is ( 5.5 + 6.7 + 6.5 + 11.7 =) 30.4%. Complementary the percentage off the diagonal is 69.6%.

Step 3: compute the kappa-coefficient by:

In this case it is: ( ( 75.8 – 30.4 ) / 69.6 = ) 0.65.

Interpreting the Kappa-coefficient

If Kappa is less than 0, it is a poor score.

A Kappa between 0 and 20 is said to be slight.

Between 21 and 40 it is fair.

Between 41 and 60 it is moderate.

Between 61 and 80 it is substantial.

Above 80 is an almost perfect score.

So in our example the computed kappa of .65 is substantial.

Related topics to Cohen's Kappa:

• Kendall’s tau
• Phi-coefficient
• Cramer´s V

All these tests are clearly explained in in our SPSS-tutorials.

Return to the index of this dictionary